Integracion por partes video 11

Los principales adelantos en integración vinieron en el siglo XVII con la formulación del teorema fundamental del cálculo, realizado de manera independiente por Newton y Leibniz. El teorema demuestra una conexión entre la integración y la derivación. Esta conexión, combinada con la facilidad, comparativamente hablando, del cálculo de derivadas, se puede usar para calcular integrales. 

Aunque Newton y Leibniz proporcionaron un enfoque sistemático a la integración, su trabajo carecía de un cierto nivel de rigor. Es memorable el ataque del obispo Berkeley calificando los infinitesimales como los "fantasmas de las cantidades que se desvanecen". El cálculo adquirió una posición más firme con el desarrollo de los límites y, en la primera mitad del siglo XIX, recibió una fundamentación adecuada por parte de Cauchy. La integración fue rigurosamente formalizada por primera vez por Riemann, empleando límites. 

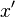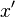Isaac Newton usaba una pequeña barra vertical encima de una variable para indicar integración, o ponía la variable dentro de una caja. La barra vertical se confundía fácilmente con o , que Newton usaba para indicar la derivación, y además la notación "caja" era difícil de reproducir por los impresores; por ello, estas notaciones no fueron ampliamente adoptadas.

La notación moderna de las integrales indefinidas fue presentada por Gottfried Leibniz en 1675.Para indicar summa (en latín, "suma" o "total"), adaptó el símbolo integral, "∫", a partir de una letra S alargada. La notación moderna de la integral definida, con los límites arriba y abajo del signo integral, la usó por primera vez Joseph Fourier en Mémoires de la Academia Francesa, alrededor de 1819–20, reimpresa en su libro de 1822. En la notación matemática en árabe moderno, que se escribe de derecha a izquierda, se usa un signo integral invertido .