Si de cada vértice de un polígono regular parten exactamente 15 diagonales, la medida de los ángulos internos de ese polígono, en radianes, es:
A) 17π/10
B) 11π/12
C) 7π/8
D) 6π/7
E) 8π/9
Pregunta tomada en el Examen de Admisión UNAC 2012 I - Universidad Nacional del Callao.
Vídeos con problemas resueltos de matemática de secundaria, bachillerato y universidad.
sábado, 29 de diciembre de 2012
viernes, 28 de diciembre de 2012
Mínimo Valor Función Exponencial
El menor valor asumido por la función f(x) = (1/2)(3 - x^2); ∀x∈ℛ es:
A) 1/4
B) 1/2
C) 1/8
D) 8
E) 4
Preguntas del Examen de Admisión UNAC 2012-I - Universidad Nacional del Callao.
A) 1/4
B) 1/2
C) 1/8
D) 8
E) 4
Preguntas del Examen de Admisión UNAC 2012-I - Universidad Nacional del Callao.
Máximo valor expresión algebraica
Si "x" toma un valor entero entre 4 y 20, ademas "y" toma un valor entero entre 1 y 9, ¿cuál es el máximo valor de la expresión x-1/y?
A) 153/8
B) 151/8
C) 9/2
D) 39/8
E) 37/2
..
Pregunta tomada en el Examen de Admisión UNAC 2012-I - Universidad Nacional del Callao.
A) 153/8
B) 151/8
C) 9/2
D) 39/8
E) 37/2
..
Pregunta tomada en el Examen de Admisión UNAC 2012-I - Universidad Nacional del Callao.
Problema Inecuacion con Factorial
Si log2 = 0,30 y log3 = 0,47 , se concluye que el menor número entero n que satisface la inecuación:
105(n!) ≤ 3·(2·4·6·8 ...(2n)) es igual a:
A) 17
B) 15
C) 16
D) 14
E) 13
..
Pregunta tomada en el examen de Admisión UNAC 2012 I - Universidad Nacional del Callao.
105(n!) ≤ 3·(2·4·6·8 ...(2n)) es igual a:
A) 17
B) 15
C) 16
D) 14
E) 13
..
Pregunta tomada en el examen de Admisión UNAC 2012 I - Universidad Nacional del Callao.
Examen de Admisión UNAC 2010-II - Solucionario - Universidad Nacional del Callao
Enunciados de las Preguntas del Examen General de Admisión.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2010 II - Solucionario del Examen de Admisión UNAC 2010 II - Universidad Nacional del Callao.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2010 II - Solucionario del Examen de Admisión UNAC 2010 II - Universidad Nacional del Callao.
Examen de Admisión UNAC 2010-I - Solucionario - Universidad Nacional del Callao
Enunciados de las Preguntas del Examen General de Admisión.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2010 I - Solucionario del Examen de Admisión UNAC 2010 I - Universidad Nacional del Callao.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2010 I - Solucionario del Examen de Admisión UNAC 2010 I - Universidad Nacional del Callao.
jueves, 27 de diciembre de 2012
Examen de Admisión UNAC 2011-II - Solucionario - Universidad Nacional del Callao
Enunciados de las Preguntas del Examen General de Admisión.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2011 II - Solucionario del Examen de Admisión UNAC 2011 II - Universidad Nacional del Callao.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Examen de Admisión UNAC 2011 II - Solucionario del Examen de Admisión UNAC 2011 II - Universidad Nacional del Callao.
Examen de Admisión UNAC 2011-I - Solucionario - Universidad Nacional del Callao
Enunciados de las Preguntas del Examen General de Admisión.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Soluciones de las preguntas.
Examen de Admisión UNAC 2011 I - Solucionario del Examen de Admisión UNAC 2011 I - Universidad Nacional del Callao.
Contenido del Examen: Razonamiento Verbal, Analogías, Oraciones Incompletas, Eliminación de Oraciones, Plan de Redacción, Razonamiento Matemático, Física, Química, Biología, Lenguaje, Literatura, Historia Universal, Historia del Perú, Economía, Educación Cívica, Geografía, Filosofía y Lógica.
Soluciones de las preguntas.
Examen de Admisión UNAC 2011 I - Solucionario del Examen de Admisión UNAC 2011 I - Universidad Nacional del Callao.
miércoles, 5 de diciembre de 2012
Diagrama de Venn Problema Resuelto
De un grupo de alumnos de grado 11, se sabe que el 25% de los que
aprueban matemáticas, aprueban física y que la mitad de los que
aprueban matemáticas aprueban física. Si se sabe que el 25% de los
alumnos no aprueban matemáticas y no aprueban física, entonces, el
porcentaje de alumnos que aprueban matemáticas y física a la vez es:
| A) 15% | B) 12% | C) 20% | D) 18% |
Problema Diagrama de Venn
En una academia de baile existen personas que practican distintas
categorías de baile de los cuales 24 no les gusta la salsa, 10 les
gusta el bolero y el merengue, 44 no les gusta el bolero, 6 no les gusta
ni la salsa ni el merengue, 40 les gusta el bolero o el merengue, a
ninguno les gusta el bolero o la salsa solamente, 16 no les gusta el
bolero ni la salsa.
Responda:
1) Cuántos les gusta solamente una categoría?
2) Cuántos les gusta por lo menos dos categorías?
3) Cuántos no bailan merengue o bolero?
--
Responda:
1) Cuántos les gusta solamente una categoría?
2) Cuántos les gusta por lo menos dos categorías?
3) Cuántos no bailan merengue o bolero?
--
Los diagramas de Venn son ilustraciones usadas en la rama de la Matemática y Lógica de clases conocida como teoría de conjuntos. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas elementos en conjuntos, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos.
Palabras clave: problema de conjuntos resuelto aplicando Diagramas de Venn Euler - Nivel Intermedio Avanzado - ejercicio difícil - ejercicio de conjuntos.
sábado, 1 de diciembre de 2012
Integral Sustitución Trigonométrica 02
Ejemplos Resueltos:
Ejemplo 01
1. 
- Sea
![$\displaystyle {x = 2\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img635.gif)

Luego:


Sustituyendo



Ejemplo 02
2. 
Sea![$\displaystyle {x = \sqrt{6}\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img644.gif)

Luego:
![$\displaystyle {\sqrt{x^{2}+6} = \sqrt{6\;sec^{2}\theta} = \sqrt{6}\;sec\;\theta...
...heta>0 si \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[\right)}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img647.gif)
Sustituyendo


![$\displaystyle {= 6 \left[\frac{1}{2}(sec\;\theta\;tan\;\theta) + ln\;\vert sec\...
...eta + tan\;\theta\vert\right] -6\;ln\;\vert sec\;\theta + tan\;\theta\vert + C}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img650.gif)



Ejemplo 03
Sea3. 
![$\displaystyle {x = \frac{3}{2}\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img655.gif)

Luego



Sustituyendo


Como
Por tanto:
 de la sustitución inicial
de la sustitución inicial


Ejemplo 04
4. 
- Sea
![$\displaystyle {x = \sqrt{3}\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img667.gif)

Luego

Sustituyendo






Como entonces
entonces

Por lo que:

se obtiene:  Por último:
Por último:

Integral Sustitución Trigonométrica 01
La integración por sustitución trigonométrica sirve para integrar funciones que tienen la forma
 ,
, 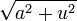 y
y 
Ejemplos:
Ejemplo 1
![$\displaystyle {\int \sqrt{16 - x^{2}}\;dx\; x \varepsilon ]-4,4[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img568.gif)
Sea con
con
![$\displaystyle {\theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img570.gif)

Luego:

Sustituyendo:





Como entonces
entonces
 y
y

Además por lo que
por lo que

Estos resultados también pueden obtenerse a partir de la figura siguiente:
Por último:



Ejemplo 2
Sea2. ![$\displaystyle {\int \frac{dx}{x\sqrt{25-4x^{2}}},\; x \varepsilon \left]\frac{-5}{2},\frac{5}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img585.gif)
![$\displaystyle {x = \frac{5}{2}\;sen\;\theta,\; \theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img586.gif)

Luego


Sustituyendo



Como entonces
entonces
 por lo que puede utilizarse la siguiente figura
para dar el resultado final:
por lo que puede utilizarse la siguiente figura
para dar el resultado final:


- Luego:

Ejemplo 3
Sea3. ![$\displaystyle {\int \frac{x^{2}\;dx}{\sqrt{4-x^{2}}},\; x \varepsilon ]-2,2[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img599.gif)
![$\displaystyle {x = 2\;sen\;\theta\; \hspace{2cm} \theta\;\varepsilon
\left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img600.gif)

Además:

Sustituyendo:






Ejemplo 4
4.![$\displaystyle {\int \frac{dx}{(5-x^{2})^{\frac{3}{2}}},\; x \varepsilon ]-\sqrt{5},\sqrt{5}[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img610.gif)
- Sea
![$\displaystyle {x = \sqrt{5}\;sen\;\theta\; \hspace{2cm} \theta\;\varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/integral_indefinida/html/img611.gif)

Luego


Sustituyendo



pues y
y

También puede utilizarse:

Suscribirse a:
Entradas (Atom)