sábado, 1 de diciembre de 2012

Integral Sustitución Trigonométrica 01







La integración por sustitución trigonométrica sirve para integrar funciones que tienen la forma
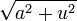\sqrt {a^2 - u^2} , \sqrt{a^2 + u^2} y \sqrt{u^2 - a^2}
Este método se basa en el uso de triángulos rectángulos, el teorema de Pitágoras e identidades trigonométricas.

Ejemplos:

Ejemplo 1


$\displaystyle {\int \sqrt{16 - x^{2}}\;dx\; x \varepsilon ]-4,4[}$
Sea $\displaystyle {x = 4\;sen\;\theta}$ con $\displaystyle {\theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = 4\;cos\;\theta\; d \theta}$

Luego: $\displaystyle {16-x^{2} = 16-16\;sen^{2}\theta = 16\;(1-sen^{2}\theta) = 16\;cos^{2}\theta}$

$\displaystyle {\sqrt{16-x^{2}} = 4\;cos\;\theta}$

Sustituyendo:

$\displaystyle {\int \sqrt{16-x^{2}}\;dx = \int 4\;cos\;\theta \cdot 4\;cos\;\theta\;d\theta = 16\int cos^{2}\theta\;d\theta}$

$\displaystyle {= 16\int \frac{1+cos\;2\theta}{2}\;d\theta = 8\int (1+cos\;2\theta)\;d\theta}$

$\displaystyle {= 8\;(\theta + \frac{1}{2}\;sen\;\theta) + C}$

$\displaystyle {= 8\theta + 4\cdot 2\;sen\;\theta\;cos\;\theta + C}$

$\displaystyle {= 8\theta + 8\;sen\;\theta\;cos\;\theta + C}$

Como $\displaystyle {x = 4\;sen\;\theta}$ entonces $\displaystyle {sen\;\theta = \frac{x}{4}}$ y $\displaystyle {\theta = arcsen\left(\frac{x}{4}\right)}$

Además $\displaystyle {\sqrt{16-x^{2}} = 4\;cos\;\theta}$ por lo que $\displaystyle {cos\;\theta = \frac{\sqrt{16-x^{2}}}{4}}$

Estos resultados también pueden obtenerse a partir de la figura siguiente:
Por último:

$\displaystyle {\int \sqrt{16-x^{2}}\;dx = 8\;\theta + 8\;sen\;\theta\;cos\;\theta + C}$

$\displaystyle {=8\;arcsen\left(\frac{x}{4}\right) + 8\cdot \frac{x}{4}\cdot \frac{\sqrt{16-x^{2}}}{4} + C}$

$\displaystyle {\int \sqrt{16-x^{2}}\;dx = 8\;arcsen\left(\frac{x}{4}\right) + \frac{x\sqrt{16-x^{2}}}{2} + C}$



Ejemplo 2

2. $\displaystyle {\int \frac{dx}{x\sqrt{25-4x^{2}}},\; x \varepsilon \left]\frac{-5}{2},\frac{5}{2}\right[}$
Sea $\displaystyle {x = \frac{5}{2}\;sen\;\theta,\; \theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$

$\displaystyle {dx = \frac{5}{2}\;cos\;\theta\;d\theta}$

Luego $\displaystyle {25-4x^{2} = 25-4\cdot \frac{25}{4}\;sen^{2}\theta = 25-25\;sen^{2}\theta}$

$\displaystyle {25-4x^{2} = 25(1-sen^{2}\theta) = 25\;cos^{2}\theta}$

$\displaystyle {\sqrt{25-4x^{2}} = 5\;cos\;\theta}$

Sustituyendo

$\displaystyle {\int \frac{dx}{x\sqrt{25-4x^{2}}} = \int \frac{\frac{5}{2}\;cos\... ...sen\;\theta\cdot 5\;cos\;\theta} = \frac{1}{5}\int \frac{d\theta}{sen\;\theta}}$

$\displaystyle {=\frac{1}{5}\int csc\;\theta\;d\theta}$

$\displaystyle {=\frac{1}{5} \;ln\vert csc\;\theta - cot\;\theta\vert + C}$

Como $\displaystyle {x = \frac{5}{2}\;sen\;\theta}$ entonces $\displaystyle {sen\;\theta = \frac{2x}{5}}$ por lo que puede utilizarse la siguiente figura para dar el resultado final:

$\displaystyle {csc\;\theta = \frac{1}{sen\;\theta} = \frac{1}{\frac{2x}{5}} = \frac{5}{2x}}$
 
Luego:

$\displaystyle {\int \frac{dx}{x\sqrt{25-4x^{2}}} = \frac{1}{5}\;ln\left\vert\frac{5}{2x} - \frac{\sqrt{25-4x^{2}}}{2x} \right\vert + C }$


Ejemplo 3

3. $\displaystyle {\int \frac{x^{2}\;dx}{\sqrt{4-x^{2}}},\; x \varepsilon ]-2,2[}$
Sea $\displaystyle {x = 2\;sen\;\theta\; \hspace{2cm} \theta\;\varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = 2\;cos\;\theta\;d\theta}$

Además: $\displaystyle {4-x^{2} = 4-4\;sen^{2}\theta = 4\;cos^{2}\theta}$

$\displaystyle { \sqrt{4-x^{2}} = 2\;cos\;\theta}$

Sustituyendo:

$\displaystyle {\int \frac{x^{2}\;dx}{\sqrt{4-x^{2}}} = \int \frac{(2\;sen\;\theta)^{2}\;2\;cos\;\theta\;d\theta}{2\;cos\;\theta}= 4 \int sen^{2}\theta \;d\theta}$

$\displaystyle {= 4\int \frac{1-cos\;2\theta}{2}\;d\theta = 2 \int (1 - cos\;2\theta)\;d\theta}$

$\displaystyle {= 2\left(\theta - \frac{1}{2}\;sen\;2\theta\right) + C}$

$\displaystyle {= 2\theta - 2\;sen\;\theta\;cos\;\theta + C}$

$\displaystyle {= 2\;arcsen\left(\frac{x}{2}\right) - 2\;\cdot \frac{x}{2} \cdot \frac{\sqrt{4-x^{2}}}{2} + C}$

$\displaystyle {= 2\;arcsen\left(\frac{x}{2}\right) - \frac{x\;(4-x^{2})}{2} + C}$


Ejemplo 4


4.		 $\displaystyle {\int \frac{dx}{(5-x^{2})^{\frac{3}{2}}},\; x \varepsilon ]-\sqrt{5},\sqrt{5}[}$


Sea $\displaystyle {x = \sqrt{5}\;sen\;\theta\; \hspace{2cm} \theta\;\varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$

$\displaystyle {dx = \sqrt{5}\;cos\;\theta\;d\theta}$

Luego $\displaystyle {5-x^{2} = 5-5\;sen^{2}\theta = 5\;cos^{2}\theta}$

$\displaystyle {(5-x^{2})^{\frac{3}{2}} = (5\;cos^{2}\theta)^{\frac{3}{2}} = \sqrt{(5\;cos^{2}\theta)^{3}}}$

$\displaystyle {(\sqrt{5}\;cos\;\theta)^{3} = 5\;\sqrt{5}\;cos^{3}\theta}$

Sustituyendo

$\displaystyle {\int \frac{dx}{(5-x^{2})^{\frac{3}{2}}} = \int \frac{\sqrt{5}\;c... ...} \int \frac{d\theta}{cos^{2}\theta} = \frac{1}{5} \int sec^{2}\theta\;d\theta}$

$\displaystyle {= \frac{1}{5}\;tan\;\theta + C}$

$\displaystyle {= \frac{1}{5}\cdot \frac{x}{\sqrt{5-x^{2}}} + C}$

pues $\displaystyle {sen\;\theta = \frac{x}{\sqrt{5}}}$ y $\displaystyle {cos\;\theta = \frac{\sqrt{5-x^{2}}}{\sqrt{5}}}$

También puede utilizarse:

Publicado por en 15:14

1 comentario:

  1. Unknown2 de mayo de 2013, 4:30

    Por qué hizo el artificio si la ∫secΘdΘ es directa y su valor es:
    Ln(secΘ + tanΘ) + C

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)