Integrales de la forma tann(x)*secm(x)
Integrar tan2(x)*sec4(x)
Integral que contiene potencias de senos y cosenos 
- En general, se intenta escribir un integrando en el que intervienen potencias de seno y coseno en una forma donde se tiene sólo un factor seno (y el resto de la expresión en términos de coseno) o sólo un factor coseno (y el resto de la expresión en términos de seno).
- La identidad
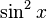



 permite convertir de una parte a otra entre potencias pares de seno y coseno.
permite convertir de una parte a otra entre potencias pares de seno y coseno.
- Existen 3 casos:
Cuando n es impar
Cuando , podemos apartar un factor del seno y sustituirlo por la identidad
, podemos apartar un factor del seno y sustituirlo por la identidad 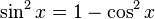 para poder expresar los factores restantes en términos del coseno:
para poder expresar los factores restantes en términos del coseno:Al tener el integral de esta forma se puede resolver por medio de sustitución haciendo
 ,
, 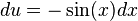 . Como en la expresión no tenemos un
. Como en la expresión no tenemos un 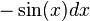 multiplicamos ambos lados por
multiplicamos ambos lados por  y nos queda la expresión
y nos queda la expresión  que ya podemos sustituir:
que ya podemos sustituir:Cuando m es impar
Cuando , podemos de la misma manera apartar un factor de coseno y emplear
, podemos de la misma manera apartar un factor de coseno y emplear  para poder expresar los factores restantes en términos del
para poder expresar los factores restantes en términos del  :
:al hacer
 y
y 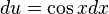 tendríamos
tendríamosCuando m y n son pares
Cuando dichas potencias son pares a la vez y
y  , podemos aplicar las identidades de la mitad de ángulo:
, podemos aplicar las identidades de la mitad de ángulo:sería igual a:
Ejemplo #1
- Solución Lo primero que tenemos que ver es que la potencia impar la tiene la función seno, esto nos hace notar que estamos en el primer caso que describimos arriba, entonces aplicamos el algoritmo,
Sustituyendo
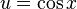 , tenemos
, tenemos  luego:
luego:









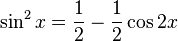
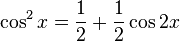



![\int [\frac{1}{2} + \frac{1}{2}\cos 2x]^{p}\;
[\frac{1}{2} - \frac{1}{2}\cos 2x]^{k} dx](http://upload.wikimedia.org/math/f/8/a/f8ad147bc91a1a82fa5309934f92f7e2.png)



No hay comentarios:
Publicar un comentario