Problemas con Planteamiento Ecuaciones - Curso Virtual Razonamiento Numérico

Plantear la ecuación equivale a expresar un enunciado (problema) al lenguaje matemático. Debemos que recordar que una ecuación está constituida por incognitas y datos.

Para resolver un problema mediante planteamiento de ecuaciones, en forma general, podemos distinguir los siguientes pasos:
  1. Lectura del enunciado
  2. Identificación de datos e incógnitas.
  3. Identificación de una relación entre datos e incógnitas llamada también: planteo de ecuación.
  4. Resolución de la ecuación.
  5. Verificación de los resultados obtenidos.
  6. Interpretación de los resultados.
A continuación veremos ejemplos de como realizar el planteamiento de una ecuación.

Planteamiento de Ecuaciones (Ecuaciones de primer grado)
Problemas Modelo
P1) La suma de tres números es 47, el segundo número es el triple del primero y el tercero excede en 12 al segundo. ¿Cuáles son dichos números?
P2) La suma de cuatro números consecutivos es 34. ¿Cuáles son dichos números?
P3) Un rectangulo mide 28 cm de perímetro. Si la base excede en 2 cm a la altura. ¿Cuáles son las dimensiones del rectángulo?
P4) José tiene un paquete de hojas. Le dío una tercera parte del paquete a María y Ana se quedó con la cuarta parte de lo que le sobraba. Karen tomó un quinto del resto. Si a José le quedarón 20 hojas. ¿Cuántas hojas tenía el paquete?



P5) La edad de Jimena es tres veces la de su hermano Juan. En cuatro años, la suma de sus edades será igual  a la mitad de la de su padre en ese entonces, su padre tiene ahora 52 años. ¿Cuántos años tiene ahora   Juan y Jimena?

A) 3 y 9

B) 4 y 12

C) 5 y 15

D) 6 y 18

Tarea 1
Utilizar como guía los problemas anteriores, para resolver los siguientes problemas.

Problema 1
La suma de tres números impares consecutivos es igual a 99. Halle la suma de los dos números mayores.

A) 68

B) 69

C)65

D) 70

E) 66

Problema 2
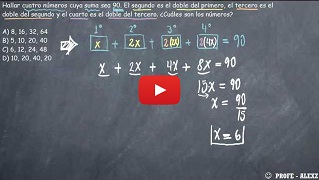
Hallar cuatro números cuya suma sea 90. El segundo es el doble del primero, el tercero es el doble del segundo y el cuarto es el doble del tercero. ¿Cuáles son los números?
A) 8, 16, 32, 64     B) 5, 10, 20, 40     C) 6, 12, 24, 48     D) 10, 20, 40, 20

Problema 3
Al multiplicar un cierto número por 81 este aumenta en 154000. ¿Cuál es le dicho número?
A) 1500     B) 1925     C) 1230     D) 4000     E) 1845

Problema 4
Juan tiene el triple de la edad de Luis. Si Juan tuviera 9 años menos y Luis 21 años más, ambas edades serían iguales. La edad de Juan, en años, es:

A) 40

B) 45

C) 38

D) 48

E) 29

Problema 5
Si la diferencia de dos números es 14560 y el duplo del mayor es 60000 ¿En cuánto excede el  número 76543 al menor de los dos números?
A) 61103     B) 61983     C) 60000     D) 62104     E) 31103

Problema 6
Entre tres alumnas tienen 28 libros. Bety tiene 3 menos que Ana y Caty tiene 2 menos que Bety. ¿Cuántos tiene Caty?
A) 7     B) 8     C) 2     D) 5     E) 6

Problema 7
Tenemos tres números: el segundo es 5 unidades más que el primero y el tercero es el doble de la suma de los dos primeros. Si la suma de los tres es 75, ¿Cuál es el segundo?
a) 6     b) 10     c) 15     d) 30     e) 50

Problema 8
En un examen de 20 preguntas, por cada pregunta acertada dan 3 puntos y por cada pregunta fallada (equivocada o no contestada) quitan 2. ¿Cuántas preguntas ha acertado y cuántas ha fallado un alumno que ha obtenido un resultado de 15 puntos?
a) Acierta 11 y falla 8         b) Acierta 11 y falla 10          c) Acierta 9 y falla 8
d) Acierta 9 y falla 11         e) Acierta 11 y falla 9

Problema 9
En 1977 Ricardo tenía 20 años y sus hermanos 6 y 7 años respectivamente, ¿cuál es el menor número  de años que debe transcurrir a partir de ese año para que la edad de Ricardo llegue a ser menor que  la suma de las edades que tendrán sus dos hermanos?

A) 28

B) 16

C) 9

D) 8

E) 7

Problema 10
La suma de tres números impares positivos y consecutivos excede al mayor de ellos en 28 unidades. Halle el producto de los tres números impares menos el producto de los números pares que se encuentran entre ellos.
A) 3091     B) 4621     C) 6459     D) 2369     E) 1512

Problema 11
En un examen de admisión de 100 preguntas, Porfirio obtiene 4 puntos por cada respuesta correcta pero pierde 2 puntos por cada respuesta errada. Si después de haber resuelto el examen obtiene 88 puntos, ¿cuántas preguntas respondió correctamente, sabiendo que desarrolló todo el examen?
A) 45     B) 48     C) 54     D) 53     E) 46

Problema 12
Estoy leyendo un libro de 450 hojas. Si lo que he leído es la tercera parte de lo que me falta por leer, 
¿Cuál es la siguiente página que leeré?

A) 225

B) 224

C)351

D) 226

E) 301

Problema 13
Daniela divide el dinero que tiene en su cartera entre 100, resulta un número entero N. Si da N billetes de $ 20 a un mendigo, aún le quedan $ 1 440. ¿Cuánto tenía en su cartera?
A. $ 1 680     B. $ 1 800     C.$ 1 720     D. $ 960     E. $ 1 840

Problema 14
Si fuera 5 horas más de lo que es, faltaría para acabar el día, el triple de las horas que habían transcurrido hasta hace 3 horas. ¿Qué hora es?
A) 6:40 am     B) 6:50 am     C) 7:00 am     D) 7:10 am     E) 7:20 am

Problema 15
Miguel tiene 2 años más que su hermano José y la edad del padre es el cuádruplo de la edad de su hijo José. Si hace 5 años la suma de las edades de los tres era 77 años, ¿Cuántos años tiene actualmente José?
A) 15 años     B) 12 años     C) 21 años     D) 17 años     E) 14 años

Problema 16
Un empleador promete pagarle a Julio, por un año de trabajo, ocho mil cuatrocientos dólares más un  televisor. Si al cabo de ocho meses despide a Julio pagándole cuatro mil ochocientos  dólares más dos  televisores, cada uno, de igual costo que el prometido, halle el precio en dólares del televisor.

A) 500

B) 550

C)900

D) 750

E) 600

Problema 17
Falta para las 9 horas la mitad de minutos que pasaron desde las 7 horas. ¿Qué hora marca el reloj?
A) 8h 40min     B) 8h 20min     C) 7h 20min     D) 8h 10min     E) 9h 10min

Problema 18
La edad actual de una persona es el doble de otra, hace 7 años la suma de sus edades era igual al promedio de sus edades actuales disminuido en 0,5. Hallar la edad del mayor.
A) 20 años      B) 25 años         C) 16 años        D) 18 años        E) 9 años

Problema 19
En un zoológico, hay cuatro tortugas: Flash, Meteoro, Rayo y Viento. Viento tiene 32 años más que Meteoro, pero 14 menos que Flash; Rayo tiene tantos años como la suma de las edades de Viento y Meteoro. Si dentro de 25 años la suma de las edades será igual a dos siglos y medio, ¿Qué edad tiene Rayo?
A) 40 años         B) 38 años         C) 62 años         D) 48 años         E) 20 años

Problema 20
En el acondicionamiento de las aulas en la ciudad universitaria, el número de carpinteros duplica al número de electricistas. Al mes, cada carpintero gana $1 400 y cada electricista $1 200. Si en un mes la suma de los sueldos de todos ellos es $48 000, ¿Cuántos carpinteros hay?
A) 12     B) 6     C) 36     D) 24     E) 48

Planteamiento  de sistema de Ecuaciones (Sistema de ecuaciones lineales 2x2)
Problemas Modelo
1) Dos números suman 20 y su diferencia es 8. Encuentra dichos números.
2) 5 Camisas y 3 pantalones costarón  55 dólares y 4 camisas y 2 pantalones, a los mismos precios costaron 40 dólares, ¿Cuál es el precio de cada prenda?
3) Una caja registradora contiene $150 en monedas de $5 y $10. Si en total hay 21 monedas. ¿Cuántas monedas hay de cada tipo?
4) El perímetro de un rectángulo es 44m y su ancho es 2m mayor que su largo. ¿Cuáles son las dimensiones del rectángulo?



5) Por tres adultos y cinco niños se pagan 190 euros para entrar a un parque de diversiones. Si son cuatro adultos y siete niños, el valor a cancelar es 260 euros. ¿Cuál es el valor de cada entrada para adulto y para niño?



Tarea 2
Utilizar como guía los problemas anteriores, para resolver los siguientes problemas.
Problema 1
De dos números que suman 240,  uno de ellos es el cuádruple del otro. Calcular el triple de la sexta parte del menor.
A) 48   B) 16   C) 42   D) 24   E) 8

Problema 2
En una granja entre gallinas y cerdos se cuentan 100 patas y 35 cabezas. ¿Cuántos cerdos hay en la granja?
A) 15   B) 20   C) 25   D) 30   E) 35

Problema 3
El triple de un número excede a otro en 10; mientras que el triple del otro excede al primero en 26. Dar como respuesta el menor.
A) 5   B) 7   C) 9   D) 11   E) 13

Problema 4
En una isla se observa tantas alas de gaviotas como cabezas de pelicanos, una vez posadas se observan noventa patas. Determinar el numero de gaviotas.
A) 15   B) 18   C) 20   D) 25   E) 30

Problema 5
Tres jugadores A, B y C tienen cierta cantidad de dinero; A y B tienen juntos $36; A y C tienen juntos $39; B y C tienen juntos $43. ¿Cuánto tiene C?
A) $23     B) $45     C) $32     D) $40     E) $18

Problema 6
Rosa le dice a Gabriela: Yo peso 30 kg más la mitad de mi peso; y Gabriela responde: Yo peso 60 kg menos la mitad de mi peso. Determine la suma de los pesos de Rosa y Gabriela.
A) 75      B)90    C) 100    D) 120    E) 150

Problema 7
Dos ómnibus tienen 120 pasajeros, si del ómnibus con más pasajeros se trasladan los 2/5 de ellos al otro ómnibus, ambos tendrían igual número de pasajeros. ¿Cuántos pasajeros tiene cada ómnibus?
A) 70 y 50     B) 110 y 10     C) 80 y 40     D) 100 y 20     E) 90 y 30

Problema 8
En una hacienda hay vacas, caballos y cerdos. Sin contar las vacas, hay 24 animales, y sin contar los caballos, hay 36 animales, y sin contar los cerdos, hay 28 animales. ¿Cuál es el número de caballos en dicha hacienda?
A) 8     B) 6     C) 10     D) 12     E) 18


Problema 9
La edad actual de Pedro es igual a la mitad de la edad actual de Luis. Hace 12 años la edad de Pedro era la cuarta parte de la edad de Luis. ¿Hace cuántos años la edad de Pedro era la tercera parte de la edad de Luis?
A) 6     B) 9     C) 10     D) 12     E) 14

Problema 10
Un joyero fabrica un total de 16 anillos, unos de oro y otros de plata. Si vende 3 anillos de cada metal precioso, le queda un número de anillos tal que el número de los de plata es el cuádruple de los de oro. Indique la proposición verdadera referida al número de anillos que fabricó el joyero.
A) 11 anillos de oro                     B) 5 anillos de plata           C) 10 anillos de plata y 6 de oro
D) 5 anillos de oro                       E) 6 anillos de plata y 10 de oro

Problema 11
Un vendedor tiene cinco canastas que contienen 4, 5, 6, 7 y 8 huevos cada una. Cada canasta contiene solo huevos de gallina o de codorniz y el vendedor dice: “Si vendo esta canasta, me quedaría el doble de huevos de gallina que de codorniz”. Halle la cantidad de huevos que contiene la canasta a la que hace referencia el vendedor.
A) 6      B) 5      C) 7      D) 8     E) 4


Problema 12 
Henry le dice a Miguel: La suma de nuestras edades es 46 años y tu edad es el triple de la edad que  tenías cuando yo tenía el triple de la edad que tuviste cuando yo nací. Entonces Miguel tiene actualmente:
A) 12      B) 24      C) 28      D) 48     E) 34



Tarea 3
Problema 1
Si subo las escaleras de 2 en 2, doy 6 pasos más que subiendo de 3 en 3. ¿Cuántos escalones tiene la escalera?

Problema 2
Si al numerador de la fracción 3/5 se le suma un número y al denominaor se le resta el mismo número se obtiene otra fracción equivalente a la reciproca de la fracción dada. Calcular el número.

Problema 3
En una granja se tienen cerdos, patos y gallinas. Sin contar los cerdos tenemos 9 animales, sin contar los patos se tendrá 7 animales y sin contar las gallilnas tenemos 14 animales ¿Cuántos cerdos hay?
A) 6     B) 2    C) 8    D) 1    E) 1

Problema 4
Yarita al ser preguntada por la hora, responde: "quedan del dia ocho horas menos que las transcurridas", ¿Qué hora es?

Problema 5
Juan le dice a Pedro: "Dame $18000 y asi tendré doble dinero que tú", y Pedro le contesta: "Más justo es que tú me des $1500  y así tendremos los dos igual cantidad" ¿Cuánto dinero tenía Pedro?

Soluciones: Problemas 1 a 5



Problema 6 (Ecuaciones cuadráticas)
Se ha comprado con 6000 pesos cierto número de cuadernos, si cada cuaderno hubiese costado 180 pesos menos, con el mismo dinero se hubiesen podido comprar 30 cuadernos más. Calcular el número de cuadernos.
A) 40  B) 20    C) 50    D) 100    E) 80

Problema 7
En un estacionamiento se cuenta 27 vehiculos entre autos y bicicletas. Si en total se han contado 60 llantas. ¿Cuántas bicicletas hay?
A) 24  B) 25    C) 23    D) 27    E) 48

Problema 8 (Ecuaciones cuadráticas)
Varios amigos alquilaron un bus por $400 para una excursión, a pagar por partes iguales, pero faltaron dos de ellos y cada uno de los que asistieron  tuvieron que pagar $10 más. ¿Cuántos fueron a la excursión?
A) 4  B) 6    C) 8R   D) 10    E) 12

Problema 9
Lo que cobra y gasta Yarita suman $600 y están en la relación de 3 a 2. ¿En cuánto tiene que disminuir el gasto para que dicha relación sea de 5 a 3?
A) 16    B) 24    C) 32    D) 15    E) 20

Problema 10
Un estante puede guardar 24 libros de RM y 20 libros de RV o 36 de RM y 15 de RV ¿Cuántos libros de RM puede contener el estante?
A) 82     B) 86     C) 84     D) 72     E) 66

Problema 11
En un corral se observa 3 gallinas por cada 5 patos y 4 conejos por cada 3 patos. Si en total se cuentan 176 cabezas ¿Cuál es el número total de patas?
A) 412     B) 484    C) 512R     D) 521     E) 544

Soluciones: Problemas 6 a 11