Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
Métodos de Solución de Sistemas de Ecuaciones
Método de Sustitución
Explicación práctica.
Teoría y ejercicios resueltos.
Método de Eliminación (Reducción).
Explicación práctica.
Teoría y ejercicios resueltos.
Método de Igualación.
Explicación práctica.

Práctica con ejercicios resueltos
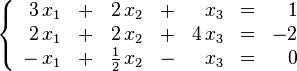

Muy sencillos. Un repaso útil. Muchas gracias.
ResponderEliminarGRACIAS PROFE ESTUVO GENIAL LA EXPLICACIÓN!!!
ResponderEliminarProblema:
ResponderEliminarFernanda pagó por una playera y un short $1 100, Adriana pagó por la misma playera y un par de tenis $1 800, mientras que Alejandra compró el short y el par de tenis en $1 700. ¿Cuál es el precio de cada artículo?
Solución:
"Fernanda pagó por una playera y un short $1 100"
=> p + s = 1100
"Adriana pagó por la misma playera y un par de tenis $1 800"
=> p + t = 1800
"mientras que Alejandra compró el short y el par de tenis en $1 700"
=> s + t = 1700
Tenemos el siguiente sistema de ecuaciones
=> p + s = 1100
=> p + t = 1800
=> s + t = 1700
Resolviendo tenemos que
=> p = 600
=> s = 500
=> t = 1200
:)
Cómo sabes el valor de cada artículo?
Eliminarresolviendo el SISTEMA de ecuaciones (:
EliminarQue sistema utilizaste?
Eliminar